Optimizing the process behavior of colloidal mixers using numerical ­simulations

Background

One of the key objectives of using colloidal mixers is to achieve a high degree of particle decomposition as a result of the mixing process. In the actual process, the degree of decomposition is very hard to evaluate and requires a sophisticated setup; in some cases, such an evaluation is not possible at all. Particle decomposition is difficult to capture visually, such as by a scanning electron microscope (SEM) (Fig. 1), because the physico-chemical processes that occur in the bentonite suspensions change the structure of the material. On the other hand, an indirect evaluation on the basis of the suspension properties is possible but relatively inaccurate, and delivers results whose validity is limited because of the structural changes that often occur even during the process. The numerical description of the process using flow simulations therefore is an appropriate alternative for investigating particle decomposition.

Methods

The activities for solving this task were divided into several stages. In the first step, the materials of various suspensions were characterized. Their flow properties were determined in experimental tests using a viscometer, and in standardized tests. On the basis of the material parameters thus obtained, various models for describing the flow behavior of the suspension were developed and integrated into the numerical model of the overall system. These models were then used to simulate the mixing process for the standard colloidal mixer at various speeds and for different suspensions. At the same time, identical tests were carried out in a physical test mixer fitted with special measuring equipment to record pressures occurring inside the mixing chamber. The results obtained were used for comparing relevant values of the real mixing process with the simulation results. In the next step, the geometrical model of the mixer paddle was parameterized in the simulation, and the paddle geometry was systematically varied. For these individual paddle shapes, the mixing process was again simulated at various speeds and for different materials, and relevant process parameters were determined. Finally, the influence of the individual geometrical parameters on the evaluation variables was analyzed statistically. The findings of this analysis served as a basis for conceiving an optimized machine design.

Calibration tests

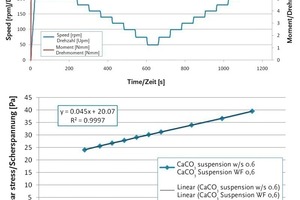
For the development of numerical models for real fluids, their characteristic parameters must first be determined. In Newtonian fluids, these include density but also viscosity as a key parameter. In Bingham fluids, yield stress is also of relevant influence. To determine these parameters, the suspensions were tested experimentally using two different methods: first, a viscometer (Viskomat NT, Schlei-binger Testing Systems) was used; second, materials were evaluated applying standardized building materials tests. The viscometer tests used a cylindrical vessel, the so-called basket cell (according to Prof. Ruprecht Vogel), and a cement paste paddle. The application of the first two geometries made it possible to determine rheological parameters. The paddle geometry was used to evaluate the material behavior at high shear rates. As suspensions, mixes of bentonite or calcium carbonate with water with varying water/solids (w/s) ratios were used. Fig. 2 shows the analysis and determination of characteristic parameters in a test of a calcium carbonate suspension with a w/s ratio of 0.6 using the cylindrical shape. The speed and gap size were used to calculate the shear rate; the shear stress was derived from the cylinder area and the measured moment. These values allow a linear regression whose functional parameters (gradient and point of intersection with the y axis) desribe the suspension characteristics. The previously made assumption that the investigated fluid was a Bingham fluid could be verified by the degree of correlation of the regression line with the experimental data (coefficient of determination).

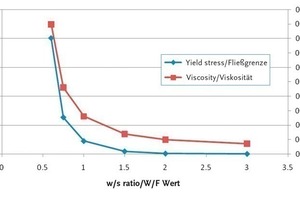
For the calcium carbonate suspension, such measurements were carried out for various w/s ratios between 0.6 and 2.0. Fig. 3 illustrates the influence of the w/s ratio on the measured yield stresses and viscosities. Additional viscometric tests were carried out at higher speeds to ensure that the behavior of the material continued to be consistent even at very high shear rates. For this purpose, the paddle geometry was used because the smaller shear gap and the greater diameter helped to achieve higher shear rates at an identical speed. Moreover, this geometry ensured uniform mixing of the suspension. These tests revealed a linear correlation between speed and moment also in the higher speed range. The Bingham fluid assumption could thus be confirmed even for high shear rates.

The bentonite suspension was more difficult to evaluate because the option of viscometric testing was limited to a short time directly after the mixing process due to its high yield stress and rheological behavior changing over time. For this reason, the viscometric tests, which took 20 to 40 minutes depending on the specific test run, were complemented by additional tests carried out after varying dwelling periods. The Haegermann cone was used for slump flow testing; a cylindrical cone served to determine flow time. The results of all three tests were combined to estimate the characteristic values of the suspension at the time of mixing (Table 1).

w/s ratioViscosity [Pas]Yield stress [Pa]200.014.4150.011511120.01223100.0125368.50.014567.50.015886.60.0211560.0315150.043226

Experimental analysis of the mixing process

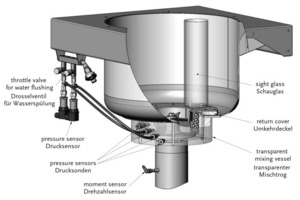
MAT Mischanlagentechnik GmbH developed a specially designed test mixer to investigate the mixing process using a physical system (Fig. 4). The lower wall section of this mixer consisted of plexiglass so that the mixing chamber was visible from outside. Initially, the motion behavior of the fluid was analyzed qualitatively at various speeds using high-speed images. However, no suspensions could be evaluated using this method because their solids content and associated turbidity make them unsuitable for optical measurements, which is why water was used as a substitute fluid. Fig. 5 shows some of the high-speed images taken at different rotational speeds. 

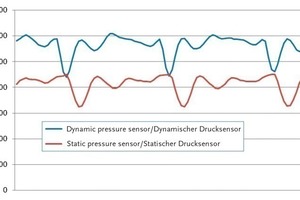
In addition, test mixer design used measuring equipment installed in the lower mixing chamber section, which included pressure sensors attached to the mixingchamber at variable heights. Sensor openings were oriented either in radial or in tangential direction. These measurements determined static pressures in the mixing chamber as a function of time and/or position. In addition, the sensors with tangential openings also captured the related dynamic pressure component. Fig. 6 shows a mean pressure series for a complete rotation involving three paddle cycles.

Besides, to speed and pressure mesurements, power consumption of the mixer was also measured. This value was used to derive the moment acting on the mixer paddle. 

Not only water was used in the tests but also the suspensions whose rheological parameters were described above. Filling level and speed were varied (see Table 2).

Process parameterRangeMixer filling level0 to 50 litersSpeed of mixing paddles0 to 960 rpmMaterialAir, water, bentonite suspension, ­calcium carbonate suspensionw/s ratio0.6 to 2 for CaCO₃; 5 to 20 for bentonite

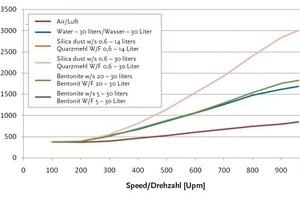
Power consumption showed a strong dependence on speed; the subsequent analysis revealed a squared correlation. Solids concentration and filling level also influenced power consumption, albeit mainly at higher speeds, whereas no significant changes were observed at very low speeds (see Fig. 7) .

Numerical simulation

The Fluent simulation software supplied by ANSYS Inc. was used for the numerical simulation of the mixing ­process.

In the first step, the mixing process was simulated as a transient process using water. In addition, a two-phase model was established to account for the air contained in the system (Fig. 8).

Further simulations reflected the material behavior of the suspension applying the Bingham model. The particles are thus represented in the fluid model of the suspension; they are not modeled as a discrete phase. At the same time, simulations were carried out in a rotating reference system. This method uses a point on the surface of the rotor as a simulation reference point. In the resulting new reference system, this causes the mixer walls to rotate whereas the actual rotor does not move. Assuming axially symmetric walls, the numerical grid in the rotating reference system remains invariable over time and thus enables the transition to steady-state simulations. While the rotating walls are modeled as a moving wall boundry condition, the centrifugal forces present in the rotating reference system are included as additional field forces. At the same time, the radial channels through which the fluid leaves the central mixing chamber disrupt the symmetry and can no longer be fully resolved, which is why they are reflected as a radially symmetrical gap in the simulation. In this gap, source terms are used to achieve a transformation from tangential to radial momentum so that the influence of these channels on the flow pattern continues to be included in the simulation. The advantage provided by this transformation is a considerable reduction in computing time: first, the transition from transient to steady-state simulation methods alone saves a major portion of the computing time required for a single simulation; second, the modeling of one third of the mixing chamber is sufficient in the above reference system due to the radial symmetry of the rotor. In total, the application of the above approaches resulted in a reduction in the computing time needed for one simulation from several days to about three hours whilst retaining the same resolution. 

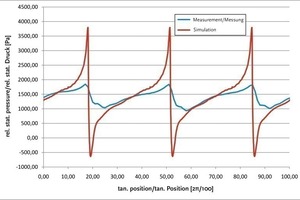
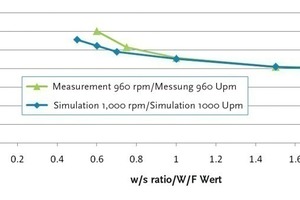
As a result of the transformation to the rotating reference system, the pressure profile generated over a circumferential line of the mixing chamber must correspond to the time-dependent signal emitted by a pressure sensor mounted at the same height in the real test. For various combinations of materials and speeds, this validation resulted in a good correlation between measurement and simulation results (Fig. 9). Likewise, close correlations were found between calculated and measured power consumption. Fig. 10 illustrates the comparison of power consumptions for a silica dust suspension with various w/s ratios at a speed of 960 rpm. The correlation of power consumption was problematic at low speeds, which was attributed to the power losses due to bearing friction, amongst other factors. A further deviation of the simulation from the measurement was recorded for pressure values at high speeds. The real-value curves show a much less marked pattern. This effect, however, can be attributed to the response time of the pressure sensor used, which makes it impossible for the sensor to process the actual pressure sufficiently quickly, and thus dampens the measured value. 

Analysis of the paddle influence in the simulation

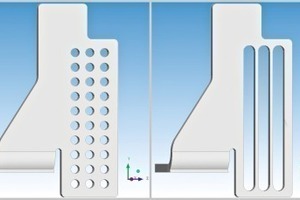
Shape and size of the used mixing paddles were parameterized and several different geometries generated to investigate the influence of the paddle geometry on the mixing and particle decomposition behavior (Fig. 11). These geometries were then used to perform numerical parameter simulations at varying speeds and for different materials. For evaluation purposes, various characteristics were determined that quantified micro-mixing and particle decomposition behavior but also the macro-mixing pattern occurring in the mixer.

Since the currently used numerical model does not consider particle fracture, the decomposition behavior was assessed using parameters with a direct influence on particle decomposition. These parameters characterize not only the likelihood of fracture but also the degree of micro mixing occurring in the mixer. In this calculation, the mean shear rates

g –= S_c g_{c, max}

n_c

and pressure gradients

Dp–= S_c Dp_{c, max}

n_c

were investigated in the mixing vessel, as well as the minimum coefficient of cavitation in the entire mixing chamber. The coefficient of cavitation

K = p – p_n

½ rU²

is obtained from the instantaneous pressure and vapor pressure of the investigated fluid and is a measure of the likelihood of cavitation to occur. In theory, cavitation may occur below a coefficient of cavitation of K = 0, but this need not necessarily happen. Significant differences were observed depending on the paddle geometry when comparing the three parameters mentioned (see Fig. 12).

To assess the macro-mixing pattern, 40,000 particles with radii between d_p,min = 1 μm and d_p,max = 100 μm were generated at a defined point in the mixing chamber. These particles move through the mixing chamber in accordance with the flow patterns calculated in the preceding step, but do not interact with each other. Using the particle distribution in the mixing chamber, the mixing quality was determined after t = [0,5s; 1,0s; 2,0s; 5,0s] and used as a parameter for macro mixing. Fig. 13 illustrates the particle distribution in the mixing chamber at a mixer speed of 200 rpm and a w/s ratio of 0.7. The defined indicators above were used to statistically analyze the influence of various geometrical parameters on the evaluation variables. As expected, speed had the most significant influence on mean pressure gradients and shear rates. When exclusively considering the geometrical parameters, with material characteristics and speeds remaining constant, the factor found to be most influential on shear rates and pressure gradients was the ratio between perforation area and total paddle area. By contrast, shape and orientation of the perforations were of relatively minor significance. Nor were any systematic correlations found between geometrical parameters and the resulting coefficients of cavitation or the achievable macroscopic mixing quality. Some of the geometries, however, resulted in a significantly lower mixing performance, which is why they will not be considered anymore in future tests.

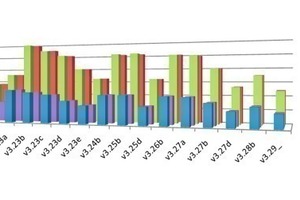
The analysis did not only include the parameters characterizing mixing quality and particle decomposition but also the torque values calculated in the simulation, which revealed differences of up to 50% (Fig. 14) depending on the paddle shape at identical speeds and for identical materials. This information will also be used in the future design of the real paddle in order to ensure that the final solution is as energy-efficient as possible.

Outlook

In the next step, the findings established in the numerical simulations will be utilized for designing new paddle geometries in order to determine possible optimization strategies. The geometries found to be most appropriate will first be tested experimentally. And additional, simulations will be performed on the basis of these test results.

Summary

The approach presented in this article enabled a thorough investigation of the flow patterns in a colloidal mixer. The characterization of the material and the validation in the real process created the basis for the numerical description of the overall system. The benefits of both approaches were combined and the reliability of simulation results ensured by repeatedly interlinking real-life testing with simulations. The combination of parameterized geometry descriptions with statistical analyses resulted in a suitable machine design that promotes particle decomposition whilst also reducing energy consumption.¢