Analyse des Trag- und Verformungsverhaltens von Sandwichbauteilen

Tragverhalten von Sandwichbauteilen

Das Tragverhalten von beliebig schichtweise aufgebauten Tragelementen wird bestimmt durch die Steifigkeit der einzelnen Schichten sowie Art und Umfang des Zusammenwirkens der einzelnen Schichten.

Im Vergleich zu den relativ steifen Deckschichten von Beton-Sandwichbauteilen sind die Eigentraganteile der Dämmschicht weitestgehend vernachlässigbar. Die Dämmschicht stellt jedoch durch Verzahnung und/oder Adhäsion einen Schubverbund zwischen den Deckschichten her, sodass Biegemomente am Gesamtquerschnitt zum Teil in ein Kräftepaar in den Deckschichten umgewandelt werden. Die Ausprägung dieses Sandwicheffektes (Membrantragwirkung) wird durch die Schubsteifigkeit der Kernschicht bestimmt und kann gezielt gesteuert werden.

Das Tragverhalten eines Sandwichelementes mit sehr schubweicher Kernschicht entspricht dem Verhalten von lose aufeinander liegenden Deckschichten. Der umgekehrte Fall führt zu schubstarr verbundenen Ober- und Untergurten, was zu der von I-Profilen bekannten hohen Biegesteifigkeit führt (Abb. 2). Die bei Sandwichbauteilen auftretenden Grenzzustände der Gebrauchstauglichkeit und der Tragfähigkeit sind aufgrund der komplexen Tragwirkung vielfältiger als bei homogenen Tragelementen. Grenzzustände der Gebrauchstauglichkeit ergeben sich hinsichtlich Verformungen und Rissbreiten, im Grenzzustand der Tragfähigkeit kann das Versagen einer der Schichten oder des Schichtverbundes maßgebend werden.

Allgemeingültiger Berechnungsansatz mit Energiemethoden

Energieprinzipien  stellen die Grundlage für analytische Methoden in der Statik dar, einen konkreten Ansatz liefert das Lagrange-Prinzip vom Minimum der potentiellen Energie: Von allen kinematisch zulässigen Formänderungen des Systems treten diejenigen ein, für die das Gesamtpotential P ein Minimum annimmt.

P = P_i + P_a ➝ Minimum(1)

Bestimmung der inneren potentiellen Energie P_i

Die bei der Deformation eines elastischen  Querschnittes verrichtete Arbeit W (Formänderungsenergiedichte) der inneren Kräfte entspricht der Integration der Spannungen über die zugehörigen Dehnungen.

Die innere potentielle Energie eines Tragwerkes ergibt sich aus der Integration der Formänderungsenergiedichte über das gesamte Tragwerk. Zur Berechnung muss das Tragwerk in Tragelemente (Index E), Querschnitte (Q) und Querschnittsteile (Schichten S) untergliedert werden.

P_i^(E) = ∫_L P_i^(Q) dx = ∫_L Σ P_i,el^(S) dx = (2)

∫_L Σ ∫_AS,i ∫₀^e_x (σ (e_x)) de_x dA_S + ∫_AS,i ∫₀^γ (τ (γ)) dγ dA_S dx

Schubstarre Schichten nehmen viel Formänderungsenergie durch Dehnungen auf, erfahren aber sehr kleine Schubverformungen mit vernachlässigbar kleinen Energieanteilen. Umgekehrt nehmen schubweiche Schichten aufgrund des geringen E-Moduls kaum Normalspannungen auf, steuern jedoch infolge großer Schubverformungen nennenswerte Formänderungsenergien bei (vgl. [9]).  

Bestimmung der äußeren potentiellen Energie P_a

Die äußere potentielle Energie ergibt sich auf Querschnittsebene als Produkt der Schnittgröße mit der zugehörigen Dehnung des Querschnittes:

Der Übergang zur Tragwerksebene erfolgt analog zum inneren Potential durch die Integration über die Länge des Tragelementes (Gleichung 3). In dieser Formulierung wird das äußere Potential als die Verschiebung der Kräfte in Richtung ihrer Wirkungslinien deutlich.

P_a^(E) = ∫_L P_a^(Q) dx = – Σ (N_j · u_j + Q_j · w_j) =

Σ ( ∫q_z,j · dx_i ) · w_j + ( ∫q_x,j · dx_i ) · u_j(3)

Schnelles Lösen der Optimierungsaufgabe mit MS Excel

Der Inhalt der mathematischen Optimierung ist die Untersuchung von Funktionalen auf Minima und Maxima, die in einer bestimmten Weise ein Optimum darstellen. Mathematisch zu erfassen ist ein Optimierungspro-blem, wenn das Ziel als Funktion eines oder mehrerer Parameter (Variablen) eindeutig formuliert werden kann. Diese wird als Zielfunktion bezeichnet. Müssen die Variablen zudem Gleichheits- oder Ungleichheitsbedingungen erfüllen, werden diese als Nebenbedingungen bezeichnet.

Die Zielfunktion entspricht in diesem Fall dem Lagrange-Gesetz vom Minimum der potentiellen Energie (Gleichung 1); variiert werden hier die Verformungen. Als Nebenbedingungen treten Verträglichkeits- und Randbedingungen auf. Verträglichkeitsbedingungen resultieren aus der Forderung nach ebenbleibenden Querschnittsteilen und stetigen Dehnungsebenen, Randbedingungen ergeben sich aus dem statischen System.

Durch die Eingabe der obenstehenden allgemeinen Beziehungen in ein Excel-Tabellenblatt steht eine Eingabemaske zur Verfügung, in welche der Benutzer lediglich Geometrie und Belastung eingeben muss. Die Lösung der Optimierungsaufgabe erfolgt mit Hilfe des in Excel integrierten Optimierungs-Algorithmus Solver „auf Knopfdruck“.

Abbildung der Materialeigenschaften

In die Berechnung der Formänderungsenergie fließen an entscheidender Stelle die Kraft-Verformungs-Gesetze der im Querschnitt enthaltenen Materialien ein. Neben den umfassend erforschten Materialgesetzen von Beton und Betonstahl kommen im Berechnungsmodell in Versuchen gewonnene Ansätze für das Materialverhalten der Dämmschicht zur Anwendung.

Die Arbeitslinie des Verbundwerkstoffes Beton verläuft sehr unterschiedlich in Druck- und Zugbereich, wobei die Zugfestigkeit aufgrund des spröden Verbundes zwischen Zementstein und Zuschlagkörnern wesentlich kleiner ausfällt. Im vorgestellten Berechnungsmodell wird für die Druckseite auf die in DIN 1045-1 verankerte, auf Grasser [2] zurückgehende Form zurückgegriffen, die den nichtlinearen Verlauf der Arbeitslinie auf der Druckseite gut wiedergibt.

Die Arbeitslinie zugbeanspruchten Betons im Zustand I wird im durch einen Polynomansatz angenähert (vgl. [4]). Im Zustand II sind gerissene Beton-Querschnittsbereiche spannungslos, das Mitwirken des Betons zwischen den Rissen wird durch die Modifizierung der Arbeitslinie des Betonstahls (s.u.) berücksichtigt.

Stahl verhält sich unter Zug- und Druckbeanspruchung nahezu gleich. Die Stahl-Arbeitslinie wird im Berechnungsmodell wie in DIN 1045-1 durch einen bilinearen Ansatz beschrieben, was genügend genaue Ergebnisse liefert.

Bei gerissenen Stahlbeton-Querschnitten wird die modifizierte Arbeitslinie des Betonstahls unter Ansatz des „verschmierten Rissmodells“ verwendet (Abb. 3). Dabei wird dem Betonstahl eine mittlere Stahlspannung so zugeordnet, dass die Energien mitwirkender Betonanteile zwischen den Rissen enthalten sind (vgl. [1]). Entsprechend werden die Spannungen von Betonbereichen mit positiven Dehnungen zu Null gesetzt, um die Energien nicht doppelt anzurechnen.

Im Rahmen der hier vorgestellten Untersuchungen wurden als Verbindungselemente zwischen den Tragschalen GFK-Stäbe vom Typ ComBAR des Herstellers Schöck eingesetzt. Stäbe aus glasfaserverstärkten Kunststoffen sind im Vergleich zu Betonstahl  bei größerer Elastizität sehr zugfest (E-Modul ca. 60.000N/mm², Zugfestigkeit ca. 1000 N/mm²). Die Arbeitslinie verläuft bis zum Versagen linear elastisch. Die Übertragbarkeit des Ansatzes für das Verbundverhalten von Stabstahl auf GFK-Stäbe wird in [5] nachgewiesen.

In Sandwichbauteilen kommen Polystyrol-Hartschaum-platten als Kerndämmung zum Einsatz, es wird hier expandierter Polystyrol-Hartschaum (EPS, z.B. Styropor) näher betrachtet. Aufgrund der sehr porösen Struktur weisen PS-Dämmstoffe nichtlineare Arbeitslinien mit vergleichsweise geringen Festigkeiten auf und kriechen stark, sodass ein Mitwirken des Dämmmaterials unter ständigen Lasten nicht angesetzt werden sollte.

Versuche zum Kraft-Verformungsverhalten der Dämmschicht

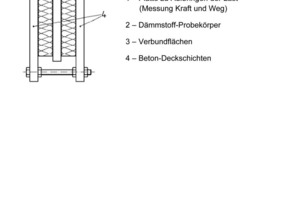
In der Dämmschicht wirken die steiferen, punktförmig angeordneten GFK-Stäbe zusammen mit dem fast vollflächig mit den Betonschalen im Verbund stehenden PS-Dämmstoff. Mit Hilfe von Scherversuchen wurden für beide Komponenten Kraft-Verformungs-Beziehungen aufgestellt, welche die Grundlage für die Ermittlung der Energieanteile der Dämmschicht darstellen.

Die geprüften Probekörper wiesen zwei außenliegende Betonschalen mit innenliegender Dämmschicht variabler Dicke auf (Abb. 4). In verschiedenen Konstellationen wurden GFK-Stäbe und die PS-Dämmstoffe einzeln geprüft. Die Unverschieblichkeit senkrecht zur Schalenebene wurde gemäß den Empfehlungen in DIN EN 12090 gewährleistet. Als Ergebnisse der Scherversuche lagen die gemessenen Scherwege und die dazu erforderliche Pressenkraft vor. Das Last-Verformungsgesetz ordnet dem Schubwinkel g der Gleitung die Kraftgröße t  zu.

Die gefundenen Materialgesetze konnten durch die Nachrechnung von Versuchen verifiziert werden, die in der Dämmschicht sowohl Dämmstoff als auch GFK-Anker aufwiesen. Dazu wurden die berechneten Schubspannungsresultierenden von Ankern und Dämmstoff superponiert. Die Resultierende entsprach der im Versuch gemessenen Pressenkraft.

Last-Verformungs-Gesetz für expandierten Polystyrol-Hartschaum (EPS)

Das Last-Verformungsverhalten der schubbeanspruchten Dämmstoffplatte ist geprägt von einem nichtlinear ansteigenden Ast bis zum Erreichen der Scherfestigkeit und einer sich anschließenden konstanten Restscherfestigkeit auf niedrigem Niveau (Abb. 5). Die Polystyrol-Platten weisen einen annähernd einheitlichen Tangentenschubmodul (G_D ≈ 0,25kN/cm²) und höhere Schubfestigkeiten bei geringeren Schichtdicken auf, was zu den dickenabhängigen Parametern in Tabelle 1 führt.

Nichtlineares Materialgesetz (Potenzfunktion):

für 0 ≤ γ ≤ γ_D,pl

t(γ) =

      t(γ) = t_D,res = const. für γ_D,pl < γ(4)

mit k_D = 1.41

Last-Verformungs-Gesetz für GFK-Anker

Für die Anker konnte durch Versuche die nachfolgende allgemeine Kraft-Verformungs-Beziehung gefunden werden.

Nichtlineares Materialgesetz (Potenzfunktion):

t(γ) = n_A ∙ t_A,max ∙ 1 – ( 1 – –––– )(5)

mit k_A=1,5

Die GFK-Anker verhalten sich mit zunehmender Dämmschichtdicke weicher (Abb. 6), was wahrscheinlich auf die zunehmende Möglichkeit von Spannungsumlagerungen bei wachsender Ankerlänge zurückzuführen ist.

Berechnungsbeispiel Sandwich-Einfeldträger

Als System wurde ein statisch bestimmt gelagerter Einfeldträger gewählt, der den in der Praxis häufig auftretenden Fall einer am oberen und unteren Rand gehaltenen geschosshohen Sandwich-Wand simuliert. Variiert wurden die Einwirkungen Temperatur und Flächenlast sowie Bauteilabmessungen und Materialfestigkeiten. Die Auswertung erfolgte anhand der vom Berechnungsmodell ausgegebenen Verläufe der Durchbiegungen, Schubverformungen und Schnittgrößen.

Die Plausibilität der Rechenergebnisse lässt sich in einem ersten Schritt gut an der berechneten Verformungsfigur des Tragelements überprüfen (Tabelle 3).

Qualitativer Vergleich der Verformungen

Als Referenz dient ein ungerissener Sandwich-Querschnitt mit 15 cm dicker Tragschale, 10 cm dicker Dämmschicht und 6 cm dicker Vorsatzschale (vgl. Abb. 7). Ein Wegfall der Schubsteifigkeit der Dämmschicht führt zu einer Zunahme der Durchbiegung um 50%. Einer Reduzierung der Tragschalendicke um 50 % führt sogar zu einer Zunahme der Durchbiegung um ca. 100 %, die Tragschalendicke wirkt sich also überproportional auf die Verformungen des Tragelementes aus.

Ferner wird an den unteren Verläufen die Steifigkeitsdegradation infolge Rissbildung sehr deutlich. Im Zustand II nimmt die Durchbiegung bei Berücksichtigung des Mitwirkens des Betons auf Zug zwischen den Rissen auf den vierfachen Wert zu. Ohne Ansatz des tension-stiffening-Effektes ist die Durchbiegung im vorliegenden Fall nochmals um 50 % größer.

Auch die Relativverschiebung der Betonschalen zueinander ist von Interesse (Abb. 8), da diese direkt die bemessungsrelevante Auslenkung der Tragelemente in der Dämmschicht wiedergibt. Zudem lassen sich hieraus Elementgrößen und Fugenmaße in der Fassade ableiten.

Ausgabe der Schnittgrößen

Die Rechenergebnisse lassen sich anhand des Betrags des Gesamtbiegemomentes in Feldmitte und der Symmetrie der Schnittgrößenverläufe verifizieren. Der „Sandwicheffekt“ äußert sich durch den Aufbau von Normalkräften in den Betonschalen und den im Vergleich zum Gesamtbiegemoment geringen Eigenbiegemomenten der Schalen (Abb. 8).

Nachrechnung von Bauteilversuchen an
Sandwichelementen

Im Rahmen der Untersuchungen wurden im Labor für konstruktiven Ingenieurbau der TU Kaiserslautern auch Bauteilversuche an vollständigen Sandwichbauteilen größerer Ausdehnungen durchgeführt (Abb. 9).

In der Nachrechnung ergibt sich eine gute Übereinstimmung der Kraft-Verformungslinien im linear-elastischen Bereich. Auch der Zeitpunkt des Übergangs in Zustand II wird gut erfasst (Abb. 10). Die Steifigkeit in Zustand II wird in der Nachrechnung geringfügig höher eingeschätzt, hier spielen die Bewehrungsstränge sowie der tension-stiffening-Effekt eine maßgebende Rolle.

Fazit und Ausblick

Die Formulierung des Verformungszustandes des Tragelementes als Optimierungsproblem auf der Grundlage von Energiemethoden ermöglicht die Analyse des Tragverhaltens von Verbundtragelementen allgemein. Der Berechnungsansatz ist auf Querschnitte weitgehend variablen Aufbaus und Materialverhaltens anwendbar und hinsichtlich der Beanspruchung und Auflagerung des Tragelementes flexibel.

Für die besonders betrachteten Stahlbeton-Sandwichelemente können die Spannungs- und Verformungszustände mit dem Berechnungsansatz weitestgehend exakt ermittelt werden. Grundlage hierfür ist die genaue Abbildung des Kraft-Verformungs-Verhaltens insbesondere der schubbeanspruchten Kernschicht. Die richtige Abbildung des tatsächlichen Last-Verformungs-Verhaltens konnte durch die Nachrechnung eines im Labor für konstruktiven Ingenieurbau der Technischen Universität Kaiserslautern durchgeführten Bauteilversuchs gezeigt werden.

Es stehen somit genauere Daten für die Bemessung von Stahlbeton-Sandwichquerschnitten zur Verfügung, was eine höhere Sicherheit gewährleisten und Spielräume für eine wirtschaftlichere Bemessung  aufzeigen kann. Zudem können Aussagen über das Auftreten und die Auswirkung der Rissbildung in den Betonschalen getroffen werden.

Die Berechnungsmodelle für die Analyse des Querschnitts bzw. des Tragelementes wurden in Form von Excel-Anwendungen weitestgehend für die einfache Verwendung aufbereitet und können als Module in umfassende VBA-Programme eingebettet werden. Auf diese Weise kann in Zukunft ein benutzerfreundliches, variables Werkzeug zur Analyse von Verbundtragelementen oder die Erarbeitung von Bemessungstabellen zur Verfügung gestellt werden.