Optimierung des Prozessverhaltens von Kolloidalmischern mittels ­numerischer Simulation

Motivation

Eine der zentralen Zielstellungen bei der Verwendung von Kolloidalmischern ist der hohe Grad des Partikelaufschlus­ses, der durch den Mischprozess erreicht werden kann. Die Bewertung des Aufschlusses im realen Prozessablauf lässt sich nur sehr schwierig und mit großem Aufwand durchführen und ist teilweise gar nicht zu realisieren. Da in den untersuchten Bentonitsuspensionen physiko-chemische Prozesse ablaufen, bei denen sich die Materialstruktur ­verändert, ist eine optische Erfassung des Partikelaufschlusses, z. B. mit einem Rasterelektronenmikroskop, schwierig (Abb. 1). Eine indirekte Untersuchung über die Eigenschaften der Suspension ist möglich, jedoch relativ ungenau, und liefert, aufgrund der sich oftmals noch im Prozess verändernden Struktur, nur begrenzt belastbare Ergebnisse. Eine geeignete Alternative zur Untersuchung des Partikelaufschlusses bietet die numerische Beschreibung des Prozesses mit Hilfe von Strömungssimulationen.

Vorgehensweise

Die Umsetzung der Aufgabenstellung unterteilt sich in verschiedene Phasen. Im ersten Schritt erfolgte eine Materialcharakterisierung verschiedener Suspensionen. Mit Hilfe experimenteller Untersuchungen am Viskosimeter sowie genormter Standardversuche wurden die Fließeigenschaften bestimmt. Aufbauend auf diesen Materialkennwerten wurden verschiedene Modelle zur Beschreibung des Fließverhaltens der Suspension entwickelt und in das numerische Modell des Gesamtsystems integriert. Auf Basis dieser Modellierung erfolgte die Simulation des Mischprozesses mit dem Standard-Kolloidalmischer bei verschiedenen Drehzahlen und mit unterschiedlichen Suspensionen. Analog dazu wurden die gleichen Versuche in einem realen Testmischer durchgeführt, der mit spezieller Messtechnik zur Aufzeichnung prozessrelevanter Drücke im Mischraum ausgestattet war. Auf Basis dieser Ergebnisse erfolgte ein Abgleich relevanter Werte zwischen realem Mischprozess und den Simulationsergebnissen. Im Anschluss wurde das Geometriemodell des Mischerpaddels in der Simulation parametrisiert und die Geometrie systematisch variiert. Für diese Paddelformen wurde bei verschiedenen Drehzahlen und Materialien der Mischprozess erneut simuliert und die relevanten Prozessgrößen ermittelt. Abschließend erfolgte eine statistische Analyse des Einflusses der verschiedenen Geometrieparameter auf die Bewertungsgrößen. Die Ergebnisse dieser Analyse dienten als Grundlage, um eine optimierte Maschinenauslegung zu entwerfen.

Kalibrierversuche

Zur Beschreibung fluider Medien in der Strömungsmechanik müssen zunächst deren Kennwerte ermittelt werden. Neben der Dichte ist dies bei Newtonschen Fluiden im ­Wesentlichen die Viskosität, bei Bingham-Fluiden hat zusätzlich die Fließgrenze einen relevanten Einfluss. Zur Ermittlung dieser Kennwerte erfolgte eine experimentelle Untersuchung der Suspensionen mit zwei verschiedenen Methoden. Zum einen wurde ein Viskosimeter (Viskomat NT von Schleibinger Testing Systems) eingesetzt, zum anderen erfolgten Materialuntersuchungen mit Standardtests aus der Untersuchung von Baustoffen. Bei den Untersuchungen am Viskosimeter wurden eine Zylindergeometrie, die Korbzelle (nach Prof. Dr.-Ing. Ruprecht Vogel) und ein Zementleimpaddel verwendet. Der Einsatz der beiden erstgenannten Geometrien ermöglichte die Bestimmung von rheologischen Parametern. Die Paddelgeometrie diente zur Untersuchung des Materialverhaltens bei hohen Scher­raten. Als Suspensionen kamen Mischungen von Bentonit oder Calciumcarbonat in Wasser bei unterschiedlichen Wasser/Feststoff-Werten (im Folgenden W/F-Wert) zum Einsatz. Abb. 2 zeigt exemplarisch die Auswertung und Kennwertbestimmung für einen Versuch mit der Zylindergeometrie für eine CaC0₃-Suspension mit einem W/F-Wert von 0,6. Anhand der Drehzahl und der Spaltgröße wird die Scherrate berechnet, und über die Zylinderfläche und das gemessene Drehmoment wird die Scherspannung ermittelt. Anhand dieser Werte kann eine lineare Regression vorgenommen werden, deren Funktionsparameter (Steigung und Schnittpunkt mit der y-Achse) die Kennwerte für die Suspension wiedergeben. Die zuvor getroffene Annahme, dass es sich bei der untersuchten Flüssigkeit um ein Bingham-Fluid handelt, kann durch die Güte der Anpassung der Regressionsgerade an die experimentellen Daten (Bestimmtheitsmaß) überprüft werden.

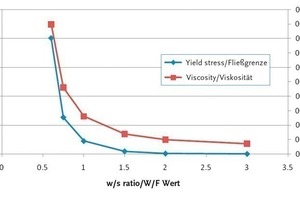
Für die CaCO₃-Suspension wurden solche Messungen mit unterschiedlichen W/F-Werten zwischen 0,6 und 2,0 durchgeführt. Der Einfluss des W/F-Wertes auf die ermittelten Fließgrenzen und die Viskositäten ist in Abb. 3 dargestellt. Um zu gewährleisten, dass sich das Material auch bei sehr hohen Scherraten ähnlich verhält, wurden zusätzlich Viskosimeterexperimente mit höheren Drehzahlen durchgeführt. Hierfür kam die Paddelgeometrie zum Einsatz, da hier durch einen kleineren Scherspalt und den größeren Durchmesser höhere Scherraten bei gleicher Drehzahl erreicht werden können. Außerdem stellt diese Geometrie eine stetige Durchmischung der Suspension sicher. Bei diesen Versuchen zeigte sich auch im oberen Drehzahlbereich eine lineare Abhängigkeit von Drehzahl und Drehmoment, so dass die Annahme eines Bingham-Fluids auch bei hohen Scherraten bestätigt wurde.

Schwieriger gestaltete sich die Untersuchung der Bentonitsuspension, da diese aufgrund ihrer hohen Fließgrenze und des zeitveränderlichen Verhaltens direkt nach dem Mischen nur eingeschränkt mit dem Viskosimeter untersucht werden konnte. Daher wurden neben den ­Viskosimeterversuchen, die je nach Versuchsdurchlauf zwischen 20 und 40 Minuten benötigten, zusätzliche experimentelle Untersuchungen nach unterschiedlichen Ruhezeiten durchgeführt. Dabei kamen der Hägermann-Trichter für das Setzfließmaß und ein zylindrischer Trichter zur Bestimmung der Auslaufzeit zum Einsatz. Durch die Kombination der Ergebnisse aller drei Versuche wurden die Kennwerte der Suspension zum Mischzeitpunkt abgeschätzt (siehe Tab. 1).

Tab. 1 Ermittelte Viskosität und Fließgrenze für Bentonit­suspensionen mit unterschiedlichem W/F-Wert.

W/F-Wert Viskosität [Pas] Fließgrenze [Pa] 200.01 4.4 15 0.0115 11 12 0.012 23 10 0.0125 36 8.5 0.014 56 7.5 0.015 88 6.6 0.02 115 6 0.03 151 50.043 226

Experimentelle Analyse des Mischprozesses

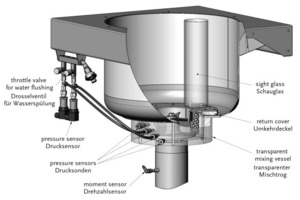
Zur Untersuchung des Mischprozesses am realen System entwickelte die MAT Mischanlagentechnik GmbH einen speziellen Versuchsmischer (Abb. 4). Die Wandung dieses Mischers bestand im unteren Bereich aus Plexiglas und ermöglichte damit einen visuellen Zugang zum eigentlichen Mischraum. Zunächst wurde das Bewegungsverhalten eines Fluids bei unterschiedlichen Drehzahlen mit Hilfe von Hochgeschwindigkeitsaufnahmen qualitativ analysiert. Dabei konnten jedoch keine Suspensionen untersucht werden, da diese aufgrund ihres Feststoffgehalts und der damit verbundenen Lichtundurchlässigkeit für optische Messungen nicht ge­eignet sind. Als Ersatzfluid kam daher Wasser zum Einsatz. Abb. 5 zeigt exemplarisch einige Einzelbilder der so entstandenen Hochgeschwindigkeitsaufnahmen.

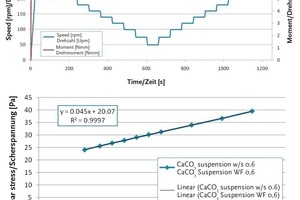
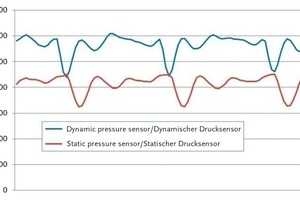
Eine weitere Adaption des Versuchsmischers bestand in der Integration von Messtechnik im unteren Mischraum. Dies umfasste die Installation von Drucksensoren, die in variablen Höhen eingesetzt werden konnten. Die Öffnungen der Sensoren wiesen dabei entweder in Radial- oder Tangentialrichtung. Aus diesen Messungen konnten zeit- bzw. positionsabhängig die statischen Drücke im Mischraum bestimmt werden. Zusätzlich erlaubten die Sensoren mit tangentialer Öffnung noch die Erfassung der entsprechenden Komponente des dynamischen Drucks. In Abb. 6 ist exemplarisch eine gemittelte Druck-Messreihe für eine komplette Rotation mit drei Paddeldurchläufen dargestellt.

Neben den Geschwindigkeits- und Druckmessungen wurde als dritte Messgröße die Leistungsaufnahme am Mischer erfasst. Mit Hilfe dieser Größe erfolgte die Bestimmung des am Mischerpaddel wirkenden Dreh­moments.

Neben den Untersuchungen mit Wasser kamen auch die zuvor bereits rheologisch beschriebenen Suspen­sionen zum Einsatz. Dabei wurden die Parameter Füllstand und Drehzahl variiert (siehe Tab. 2).

Table 2 Im Rahmen der Experimente variierte Parameter.

Prozessgröße Bereich Füllstand im Mischer 0 bis 50 Liter Drehzahl der Mischpaddel 0 bis 960 Upm Material Luft, Wasser, Bentonitsuspension, Calciumcarbonatsuspension W/F-Wert 0,6 bis 2 für CaCO₃; 5 bis 20 für Bentonit

 
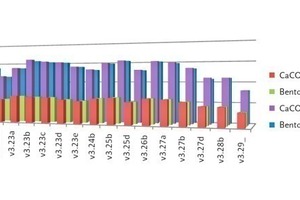
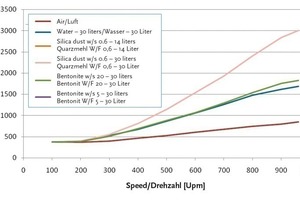
Die Leistungsaufnahme zeigte eine starke Abhängigkeit von der Drehzahl, die spätere Analyse ergab dabei einen quadratischen Zusammenhang. Feststoffkonzentration und Füllstand hatten ebenfalls einen Einfluss auf die ­Leistungsaufnahme, der sich jedoch vorrangig bei hohen Drehzahlen zeigte, während bei sehr niedrigen Drehzah­len keine signifikanten Veränderungen auftraten (siehe Abb. 7).

Numerische Modellierung

Für die numerische Modellierung des Mischprozesses kam das Simulationsprogramm Fluent der Firma Ansys Inc. zum Einsatz.

Im ersten Untersuchungsschritt wurde der Mischvorgang als instationäre Berechnung mit Wasser durchgeführt. Darüber hinaus erfolgte eine Modellierung mit einem 2-Phasenmodell zur Darstellung der im System enthaltenen Luft (Abb. 8).

In weiteren Simulationen erfolgte die Abbildung des Materialverhaltens der Suspension mit Hilfe des Bingham-Modells. Die Partikel sind damit im Fluidmodell der Suspension abgebildet und werden nicht als diskrete Phase modelliert. Gleichzeitig wurde die Simulation in einem rotierenden Bezugssystem durchgeführt. Bei diesem Verfahren wird ein Punkt auf der Oberfläche des Rotors als Bezugspunkt für die Simulation gewählt. In dem entstehenden neuen Bezugssystem rotieren damit die Mischerwände, während der eigentliche Rotor stillsteht. Unter der Annahme von rotationssymmetrischen Wänden ist das numerische Gitter im rotierenden Bezugssystem zeitlich unveränderlich und ermöglicht somit den Übergang zu stationären Simulationen. Während die rotierenden Wände als Randbedingungen mit konstanter Oberflächengeschwindigkeit in die Simulation eingebunden sind, werden die im rotierenden Bezugssystem existierenden Fliehkräfte als zusätzliche Feldkräfte abgebildet. Gleichzeitig können die radialen Strömungskanäle, über die das Fluid die zentrale Mischkammer verlässt und die einen Symmetriebruch darstellen, nicht länger voll aufgelöst werden und sind daher im Rahmen der Simulation als radialsymmetrischer Spalt abgebildet. In diesem erfolgt mittels Quelltermen eine Transformation von Tangential- in Radialimpuls, so dass der Einfluss dieser Kanäle auf das Strömungsbild in der Simulation weiterhin enthalten ist. Der Vorteil der hier beschriebenen Transformation liegt in einer deutlichen Reduzierung der Rechenzeit: zum ­einen kann schon durch den Übergang von instationären auf stationäre Simulationstechniken ein großer Teil der für eine Simulation nötigen Rechenzeit eingespart werden, zum anderen ist in dem beschriebenen Bezugssystem durch die Radialsymmetrie des Rotors die Modellierung eines Drittels des Mischraumes ausreichend. Insgesamt konnte durch Anwendung der oben beschriebenen Ansätze die für eine Simulation benötigte Rechenzeit von mehreren Tagen auf etwa 3 Stunden bei gleicher Auflösung reduziert werden.

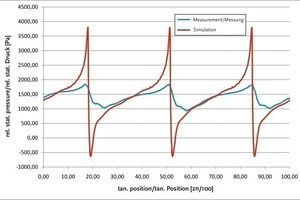
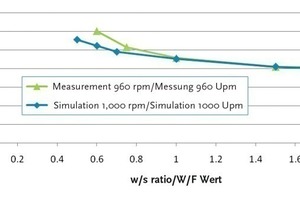
Durch die Transformation in das rotierende Bezugssystem muss das über einer Umfangslinie der Mischkammer entstehende Druckprofil dem zeitlichen Signal eines im realen Versuch in gleicher Höhe positionierten Druckaufnehmers entsprechen. Diese Validierung lieferte für verschiedene Material- und Drehzahlkombinationen gute Übereinstimmungen zwischen Experiment und Simula­tion (siehe Abb. 9). Ebenso konnten gute Übereinstimmungen zwischen der berechneten und gemessenen Leistungsaufnahme festgestellt werden. Abb. 10 zeigt den Abgleich für die Leistungsaufnahme mit Quarzmehlsuspension bei verschiedenen W/F-Werten mit einer Drehzahl von 960 Upm. Problematisch zeigte sich die Übereinstimmung der Leistungsaufnahme bei niedrigen Drehzahlen, was auf die Leistungsverluste durch Lagerreibung etc. zurückgeführt wird. Eine weitere Abweichung zwischen Simulation und Messung tritt bei hohen Drehzahlen bei den Druckwerten auf. Die Verläufe sind bei den real gemessenen Werten deutlich schwächer ausgeprägt. Dieser Effekt lässt sich jedoch durch die Trägheit des verwendeten Drucksensors erklären, welche es dem Sensor nicht ermöglicht, den realen Druck schnell genug zu verarbeiten, und somit den Messwert dämpft.

Analyse des Paddeleinflusses in der Simulation

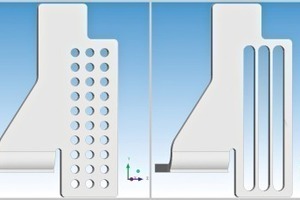
Zur Untersuchung des Einflusses der Paddelgeometrie auf das Mischungs- und Aufschlussverhalten wurden die Form und Größe der verwendeten Mischerpaddel parametrisiert und anschließend verschiedene Geometrievarianten generiert (siehe Abb. 11). Auf Basis dieser Geometrien erfolgten numerische Parameterstudien mit verschiedenen Drehzahlen und Mate­rialien. Zur Beurteilung wurden unterschiedliche Kenngrößen ermittelt, welche einerseits Mikrovermischung und Aufschlussverhalten und andererseits die im Mischer realisierte Makrovermischung quantifizierten.

Da das momentan verwendete numerische Modell Partikelbrüche nicht berücksichtigt, erfolgte die Beurteilung des Aufschlussverhaltens mit Hilfe von Kennwerten, die den Aufschluss indirekt beeinflussen. Diese Kennzahlen charakterisieren neben der Bruchwahrscheinlichkeit auch die im Mischer realisierte Mikrovermischung. Untersucht wurden dabei die durchschnittlichen Scherraten

g  = S_c g_{c, max} / n_c

und Druckgradienten

Dp  = S_c Dp_{c, max /} n_c

im Mischtrog sowie die minimale Kavitationszahl im gesamten Mischraum. Die Kavitationszahl

K = p – p_n / ½ rU²

berechnet sich aus Momentandruck und Dampfdruck des untersuchten Fluids und ist ein Maß für die Wahrscheinlichkeit des Auftretens von Kavitationsblasen. Theoretisch kann ab einer Kavitationszahl von K = 0 Kavitation auftreten, muss jedoch nicht. Beim Vergleich der drei angesprochenen Kennzahlen konnten starke Unterschiede in Abhängigkeit der Paddelgeometrie festgestellt werden (siehe Abb. 12).

Zur Beurteilung der Makrovermischung wurden in der Simulation an einer definierten Stelle im Mischraum 40.000 Partikel mit Radien zwischen d_p,min = 1 μm und d_p,max = 100 μm generiert. Diese bewegen sich aufgrund der zuvor  berechneten Strömungsverhältnisse durch den Mischraum, interagieren untereinander jedoch nicht. Anhand der Partikelverteilung im Mischraum wurde nach t = [0,5s; 1,0s; 2,0s; 5,0s] jeweils die Mischgüte bestimmt und als Kennzahl für die Makrovermischung verwendet. Die Entwicklung der Partikelverteilung im Mischraum bei einer Mischerdrehzahl von 200 Upm und einem W/F-Wert von 0,7 ist in Abb. 13 dargestellt.

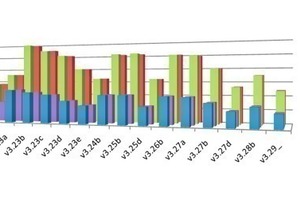
Mittels dieser Indikatoren erfolgte eine statistische Analyse des Einflusses verschiedener Geometrieparameter auf die Bewertungsgrößen. Den deutlichsten Einfluss auf mittlere Druckgradienten und Scherraten hatte erwartungsgemäß die Drehzahl. Bei ausschließlicher Betrachtung der Geometrieparameter bei konstant gehaltenen Materialeigenschaften und Drehzahlen wurden Scherrate und Druckgradient am stärksten durch das Verhältnis von Loch- zu gesamter Paddelfläche beeinflusst. Die Form und Ausrichtung der Löcher hatten dagegen nur eine geringere Bedeutung. Auch wurden keine systematischen Zusammenhänge zwischen Geometrieparametern und den sich ergebenden Kavitationszahlen bzw. der erreichbaren makroskopischen Mischgüte festgestellt. Einzelne Geometrien zeigten jedoch eine deutlich verringerte Mischleistung und werden daher in späteren Untersuchungen nicht mehr betrachtet.

Neben diesen Mischgüte und Partikelaufschluss charakterisierenden Größen wurden die in der Simulation berechneten Drehmomente in die Auswertung aufgenommen. Hierbei zeigte sich, dass bei gleicher Drehzahl und identischem Material Unterschiede von bis zu 50 % (Abb. 14) in Abhängigkeit der Paddelform auftreten. Diese Informationen werden in der späteren Auslegung des realen Paddels ebenfalls berücksichtigt werden, um so eine möglichst energieeffiziente Lösung zu gewährleisten.

Ausblick

Im nächsten Schritt sollen die auf Basis der numerischen Simulationen gewonnenen Erkenntnisse bezüglich möglicher Optimierungsstrategien in die Konstruktion neuer Paddelgeometrien einfließen. Dabei sollen die hier als am geeignetsten identifizierten Geometrien zunächst experimentell untersucht und aufbauend auf den dabei erhaltenen Ergebnissen weitere Simulationen durchgeführt werden.

Zusammenfassung

Mit Hilfe der vorgestellten Vorgehensweise konnte eine fundierte Untersuchung der Strömungsverhältnisse in einem Kolloidalmischer durchgeführt werden. Die Charakterisierung des Materials und die Validierung am realen Prozess stellten die Basis für die numerische Beschreibung des Gesamtsystems dar. Durch die wiederholte Verknüpfung zwischen realem Experiment und Simulation wurden die Vorteile beider Ansätze kombiniert und die Zuverlässigkeit der Simulationsergebnisse gewährleistet. Mit Hilfe der Kombination von parametrisierter Geo­metriebeschreibung und statistischer Auswertung konnte eine geeignete Maschinenauslegung gefunden werden, die sowohl den Partikelaufschluss begünstigt als auch die Energieaufnahme reduziert.