Ersatz von Natursand in Beton durch Brechsand mit Hilfe von nichtlinearer Modellierung

Es besteht enormer Druck, auf den Einsatz von Natur-sand in Beton zu verzichten und stattdessen Brechsand oder rezyklierte Gesteinskörnungen einzusetzen. Brechsand weist allerdings scharfe Kanten auf, wodurch nicht nur das Fließverhalten von Frischbeton beeinträchtigt wird, sondern auch die Festigkeit von Festbeton. Daher ist die Zugabe von Brechsand in großen Mengen nicht ohne weiteres möglich. Zur Bestimmung von Mischungsentwürfen, mit denen sich die Spezifikationen von Frisch- und Festbeton erfüllen lassen, muss man wissen, wie sich die Zusammensetzung des Mischungsentwurfs auf die Variablen dieser Spezifikationen auswirkt.

Wie sich in sehr vielen Fällen zeigte, sind die Auswirkungen in der Regel nichtlinear. Zudem entstehen bei Variablenpaaren übergreifende Wirkungen. Lineare statistische Verfahren sind daher zur Beschreibung dieser Zusammenhänge nicht geeignet. Nichtlineare Modelle haben sich in vielen Fällen bei der Beschreibung dieser Beziehungen aus einer begrenzten Anzahl von Experimenten als sehr effizient erwiesen. Daher werden im vorliegenden Beitrag nichtlineare Modelle zu Mörteleigenschaften aus Versuchsdaten entwickelt. Mit diesen Modellen lässt sich jetzt der Höchstanteil an Brechsand berechnen, der hinzugefügt werden kann, ohne die Eigenschaften zu beeinträchtigen.

1 Einleitung

Umweltaspekte führen zu verstärktem Druck auf die Betonhersteller, ihren Einsatze von Natursand zu verringern. Darüber hinaus sinkt die Verfügbarkeit von Sand und in vielen Ländern wurden von der öffentlichen Hand Beschränkungen zur Verwendung von Natursand auferlegt. Da Brechsand und rezyklierte Gesteinskörnungen eher weniger runde Ecken und Kanten aufweisen, führt dies zu einer geringeren Fließfähigkeit von Frischmörtel. Ein korrektes Fließverhalten ist jedoch für Vergussmaterial und selbstverdichtenden Beton unerlässlich, was den Anteil von Brechsand anstelle von tendenziell runderem Natursand einschränkt.

Ein kleiner Teil an Brechsand kann auch ohne Durchführung von Versuchen eingesetzt werden; um jedoch den maximalen Anteil von Brechsand zu ermitteln, sind genauere Kenntnisse über den Einfluss auf die Eigenschaften von Frisch- und Festmörtel erforderlich. Dies ist in erster Linie ein Problem in der Materialentwicklung und daher ist der Ansatz, der bei verschiedensten anderen Materialien verwendet wird, auch für Mörtel anwendbar.

2 Materialentwicklung

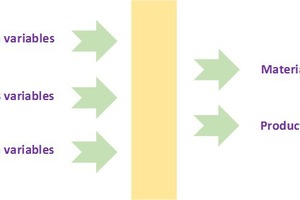
Ziel der Materialentwicklung ist in der Regel, eine Reihe von gewünschten Eigenschaften zu erreichen. Dies lässt sich jedoch nicht bei unverhältnismäßigen Kosten verwirklichen. Herstellungskosten können verschiedene Variablen umfassen, wie Rohmaterialkosten, Energiekosten, Arbeitskosten pro Gewichtseinheit oder Volumeneinheit oder die Gesamtproduktionskosten pro Gewichtseinheit oder Volumeneinheit, die finanziell tragbar sein sollten. All diese Variablen hängen von den Variablen der Zusammensetzung ab bzw. den verschiedenen Mengen der in den Prozess eingehenden Werkstoffe, den Prozessvariablen bei der Verarbeitung der Rohstoffe sowie Bemaßungsvariablen, wie Angaben zu Partikelgröße, Stärken, Durchmessern, Kanten oder Rundheit der Partikel. Die Beziehungen zwischen den Materialeigenschaften und den Variablen links in Abbildung 2 sind in der Regel nicht einfach oder linear.

Mit physikalischen Modellen lassen sich die Zusammenhänge zwischen den Materialeigenschaften und den links dargestellten Variablen kaum herstellen. Daher werden empirische oder semi-empirische Modelle verwendet. Die herkömmliche empirische Modellierung erfolgt mit Hilfe von linear statistischen Verfahren, die sich zur Beschreibung von Nichtlinearitäten nicht besonders eignen. Bei einer Vielzahl von Materialien hat sich allerdings die nichtlineare Modellierung als effektiv erwiesen. Die Leser der BFT International erinnern vielleicht an den Fachbeitrag aus dem Jahr 2015 zu selbstverdichtendem Beton [1], in dem gezeigt wurde, wie die Produktionskosten in einem Werk in Nummela, Finnland, mit Hilfe nichtlinearer Modelle drastisch gesenkt werden konnten.

3 Mathematische Modellierung mit

unterschiedlichen Ansätzen

Mathematische Modelle sind quantitative Beschreibungen von Variablen. Mit anderen Worten, sie beinhalten gebündeltes Wissen zu einem System über die quantitativen Wirkungen der ausgewählten Variablen. Es wird versucht, mit derartigen Modellen die Realität abzubilden und sofern sie von hinreichend guter Qualität sind, können sie anstelle von Versuchsreihen eingesetzt werden. Die mathematische Modellierung wird mit unterschiedlichen Ansätzen durchgeführt.

Physikalische Modelle werden durch Formilierung von Naturgesetzen in mathematischer Form entwickelt. Diese Modelle erfordern viele Annahmen und Vereinfachungen. Die Lösung dieser Gleichungen erfordert viel Zeit, wodurch sie zur Bestimmung von gültigen Werten für Prozessvariablen unpraktisch sind.

Die empirische und semi-empirische Modellierung beschreibt die Realität so wie sie beobachtet wird, ohne dass wesentliche Annahmen oder Vereinfachungen benötigt werden. Hierzu sind entweder Messungen aus Produktionsdaten oder aus Versuchsreihen erforderlich. Die empirische Modellierung wird in der Regel anhand von linearen statistischen Verfahren durchgeführt, die zur Beschreibung von Nichtlinearitäten hinsichtlich der Wirkung von Variablen nicht sehr effektiv sind. In der Natur ist nichts sehr linear und daher ist es sinnvoll, Nichtlinearitäten anhand neuer Verfahren zur nichtlinearen Modellierung zu berücksichtigen.

4 Nichtlineare Modellierung

Einer der Hauptziele dieses Fachbeitrags ist es, der nichtlinearen Modellierung in der Beton- und Mörtelindustrie mehr Aufmerksamkeit zu verschaffen. Bei der nichtlinearen Modellierung handelt es sich um empirische oder semi-empirische Modellierung, die zumindest einige Nichtlinearitäten berücksichtigt. Zu den älteren Verfahren gehören die polynomiale Regression, die lineare Regression mit nichtlinearen Termen und die nichtlineare Regression. Diese Verfahren sind im Gegensatz zu den neuen Verfahren der nichtlinearen Modellierung, die auf Nichtlinearitäten in beliebigen Formen basieren, mit mehreren Einschränkungen verbunden.

Die neuen Verfahren der nichtlinearen Modellierung, insbesondere vorwärts gerichtete neuronale Netzwerke, haben sich bei der Modellierung von Prozessen und Materialverhalten [2, 3] vor allem aufgrund ihrer universellen Approximationsfähigkeit [4] als wertvoll erwiesen. Nichtlineare Modelle lassen sich in der Regel anhand von Extrapolationsfähigkeiten mit vorwärts gerichteten neuronalen Netzwerken erstellen. Künstliche neuronale Netze bestehen aus schichtweise angeordneten Neuronen oder Knoten, die in der Regel direktional mit anderen in den angrenzenden Schichten verknüpft sind. Eine Art des vorwärts gerichteten neuronalen Netzwerks ist das Mehrschicht-Perzeptron-Netz (Abb. 3). Die nichtlineare Modellierung wird bereits erfolgreich in verschiedenen Industriezweigen eingesetzt, dazu gehören die Bereiche Zement [5], Beton [6], Glas [7], Keramik [8], Metall [9], Plastik [10], Verbundstoff [11], Gummi [12], Stromerzeugung [13], Biotechnologie [14], Halbleiter [15] sowie medizinische Materialien [16].

Entgegen der allgemeinen Auffassung, dass für neuronale Netze riesige Datenmengen nötig sind, werden hierfür in Wahrheit weniger Versuchsreihen benötigt, wenn sie geplant werden, wobei zu berücksichtigen ist, dass die Auswirkungen im Vergleich zu herkömmlichen Methoden der Versuchsplanung, basierend auf linearen statistischen Verfahren, nichtlinear sein können. Nichtlineare Modelle sind tendenziell robuster, sofern sie sorgfälltig entwickelt wurden. Die für den vorliegenden Beitrag entwickelten Modelle sorgen beispielsweise dafür, dass die Eigenschaften nicht negativ sein können. Mit linearen Regressionsmodellen könnten negative Werte leicht prognostiziert werden.

5 Versuchsdaten

Für die Entwicklung nichtlinearer Modelle werden Versuchs- oder Produktionsdaten benötigt. Für den vorliegenden Beitrag wurde ein experimenteller Ansatz bevorzugt. Insgesamt wurden 22 Versuche mit unterschiedlichen Brechsanden in verschiedenen Partikelgrößen und Rundheiten und mit unterschiedlichen Brechsandanteilen durchgeführt. Die Daten wurden zunächst vorverarbeitet und analysiert. Hierbei ist zu beachten, dass die Rundheitsfunktion nach Wadell [17] anstelle der Sphärizität, definiert durch Volumen-Oberflächen-Verhältnis, angewandt wurde, da in der Vergangenheit festgestellt wurde, dass die Rundheit besser mit den Fließeigenschaften korreliert. Die Rundheit wurde von Wadell [17] als Verhältnis von durchschnittlichem Radius der Krümmung der Umrisslinie des Partikels zum Radius des größten einbeschriebenen Kreises definiert:

wobei n die Anzahl der Ecken angibt, r_i den Radius der i^th Krümmung der Umrisslinie und r_max den Radius des größten einbeschriebenen Kreises. Rundheit wäre genau 1 bei einer perfekten Kugel und andernfalls kleiner 1.

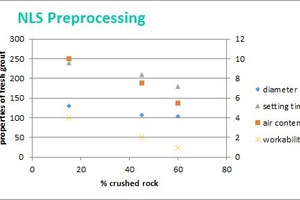
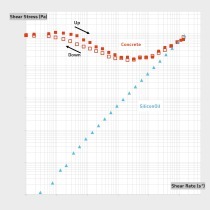
Aus den Rohdaten der Versuchsreihen ergaben sich einige eindeutige Feststellungen. So führte beispielsweise eine Erhöhung des Brechsandanteils zu geringerem Ausbreitdurchmesser, kürzerer Abbindezeit, geringem Luftgehalt und schlechter Verarbeitbarkeit, als erwartet. Dies wird anhand der in Abbildung 4 dargestellten Daten aus den drei Versuchsreihen ersichtlich. Mehrere Versuchsreihen mit unterschiedlichen Durchmessern des ersten Dezils bei ansonsten konstanten Variablen durchzuführen war schwierig. Aus dem vollständigen Datensatz wurde jedoch ersichtlich, dass der Gesamteffekt einer Erhöhung des Brechsanddurchmessers des ersten Dezils zu geringerem Ausbreitmaß, geringerem Luftgehalt, kürzerer Abbindezeit, schlechterer Verarbeitbarkeit, jedoch höherer Festigkeit nach 7 bzw. 28 Tagen führte.

6 Nichtlineare Modelle zu sechs Eigenschaften

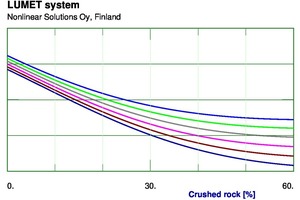
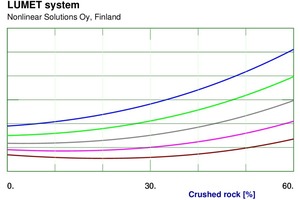
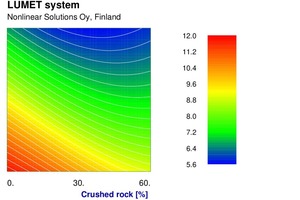
Anschließend wurden nichtlineare Modelle mit der Software NLS 020 entwickelt. Hierzu wurden mehrere Modellen mit unterschiedlichen Konfigurationen neuronaler Netze mit Einschränkungen einer oder mehrerer Gewichtungen in den Netzen erprobt. Die letztlich ausgewählten Modelle wurden anschließend in ein Lumet-System – Softwarekomponenten zur einfachen Anwendung von nichtlinearen Modellen – implementiert. Das System enthält Hilfen für verschiedene Arten von Berechnungen aus den nichtlinearen Modellen. Es ermöglicht, die Wirkung der Eingangsvariablen auf verschiedene Weise darzustellen. Abbildung 5 zeigt eine Reihe von Kurven mit unterschiedlichen Werten des Brechsanddurchmessers des ersten Dezils und stellt die Wirkung des Brechsandanteils auf das Ausbreitmaß dar. Gleichermaßen zeigt Abbildung 6 die Wirkung von Brechsandanteil auf die Druckfestigkeit nach 7 Tagen bei unterschiedlichen Werten für die Rundheit des Brechsands. Erwartungsgemäß sind die Wirkungen nicht sehr linear und lineare statistische Verfahren nicht sehr effektiv, um diese zu beschreiben.

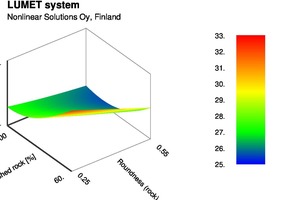
Abbildung 7 zeigt ein Konturdiagramm des Luftgehalts auf einer Ebene des Bruchsandanteils und erstem Dezil des Natursanddurchmessers. Um den Luftgehalt im akzeptablen Bereich zu halten, ist die machbare Region begrenzt. Je geringer der D10-Sand, je mehr Brechsand kann zugegeben werden. Abbildung 8 zeigt ein Oberflächendiagramm der 28-Tage-Durckfestigkeit gegenüber Brechsandanteil und Rundheit des Brechsands. Die Wirkung ist nicht nur nichtlinear, es besteht auch eine stark übergreifende Wirkung bei diesem Variablenpaar. Mit der quantitativen Kenntnis über die Wirkungen der Eingangsvariablen von Frisch- und Festmörteleigenschaften in Form von Gleichungen, kann die maximale Brechsandmenge, die anstelle von Natursand verwendet werden kann, um die Eigenschaften entsprechend den zulässigen Grenzwerten einzuhalten, jetzt einfach bestimmt werden.

7 Schlussfolgerungen

Ein höherer Anteil an Brechsand oder rezyklierten Gesteinskörnungen kann anstelle von Natursand eingesetzt werden, ohne die Eigenschaften von Frisch- und Festmörtel zu beeinträchtigen. Der Höchstanteil an Brechsand, der beigegeben werden kann, ist von der Partikelgrößenverteilung von Natursand und Brechsand abhängig sowie deren Rundheiten.

Auf Grundlage einer kleinen Versuchsreihe im Labor wurden nichtlineare Modelle entwickelt, um die Eigenschaften von Frisch- und Festmörtel in Beziehung zu dem Anteil an Brechsand, der Partikelgrößenverteilung und den Rundheiten zu setzen. Es gibt starke nichtlineare Auswirkungen einiger Variablen auf die Eigenschaften, und lineare statistische Verfahren wären nicht effizient gewesen. Ein einfaches Software-Tool wurde für den Einsatz bei Saint Gobain Weber entwickelt, das die Bestimmung der Höchstmenge an Brechsand als Ersatz von Natursand ermöglicht. Mit mehr Daten von unterschiedlichem Sand und Gesteinskörnungen, können die nichtlinearen Modelle im Laufe der Zeit noch verbessert werden.